Guppy LoRaWAN®- Tilt / Static Angle Output Examples
The tilt reporting feature in the Guppy, as of firmware v1.9, is explained in the Guppy Configuration and Usage Guide.
Here are a few pictures and examples to help you understand how the feature works.
This article deals with some static setups, and what angles they result in.
Static setup 1:
In this setup, "down" on the Guppy aligns well with gravity. We expect the angle of inclination to be close to 180°.

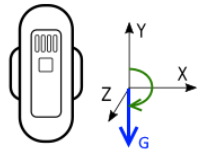
The photo above resulted in this payload: 9c7eeedc
This payload decodes to:
{
"type": "status",
"inTrip": false,
"batV": 3.092,
"temp": 23,
"manDown": false,
"inclinationDeg": 178.5,
"azimuthDeg": 330,
"xyz": {
"downUnit": [
-0.01309,
-0.9997,
0.02267
],
"azimuthDeg": [ left out ],
"inclinationDeg": [ left out ],
}
}
This matches our expectation for an inclination angle of about 180 degrees.
The azimuth angle is not significant in this case - the size of the xz vector is very small.
The down unit vector is close to -1 in the y direction, and insignificant in the other directions.
Static Setup 2:
The Guppy is lying on its side.

It may be useful to think of the Guppy's coordinate system as rotating, with gravity still down. Remember to measure:
- Inclination angle: the angle from the positive Y axis (which rotated with the Guppy) to gravity, in the X-Y plane. We'd expect that to be 90 degrees in this case.
- Azimuth angle: the angle from the positive Z axis to gravity, in the X-Z plane, following the right hand rule (right hand thumb in the direction of Y, with fingers curled around the Y axis - measure in the direction your finger point). We'd expect this to be 90 degrees too.
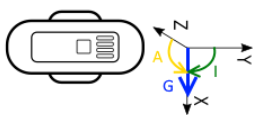
This setup resulted in this payload: 9c7e763d
This decodes to:
{
"type": "status",
"inTrip": false,
"batV": 3.092,
"temp": 23,
"manDown": false,
"inclinationDeg": 88.5,
"azimuthDeg": 91.5,
"xyz": {
"downUnit": [
0.9993,
0.02618,
-0.02617
],
"azimuthDeg": [ left out ],
"inclinationDeg": [ left out ],
}
}
This matches our expectation for an inclination angle of about 90 degrees.
The azimuth angle is also about 90 degrees.
The down unit vector is close to +1 in the x direction, which matches our expectation from the diagram.
Static Setup 3:
The Guppy is lying on its back.

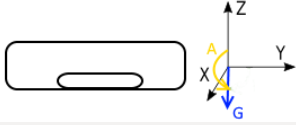
Again, think of the coordinate system rotating, and gravity as down. Gravity is more or less aligned with the Z axis, but in the negative direction. So we expect the azimuth angle to be about 180 degrees.
The inclination angle is not significant, as we expect the XY vector to be very small.
This setup resulted in this payload: 9c7d7879
{
"type": "status",
"inTrip": false,
"batV": 3.092,
"temp": 22.5,
"manDown": false,
"inclinationDeg": 90,
"azimuthDeg": 181.5,
"xyz": {
"downUnit": [
-0.02618,
6.123e-17,
-0.9997
],
"azimuthDeg": [ left out ],
"inclinationDeg": [ left out ],
}
}
As expected, the azimuth angle is close to 180 degrees.
The inclination angle happens to be 90 degrees, but the value is not significant because the XY vector is so small. (Note the E-17 on the y downUnit vector - that's a small value).
Static Setup 4:
The Guppy is at an angle to the right and backwards.

Sorry about this picture!
Again, it's useful to consider the Guppy axes rotated and gravity down.
We expect the inclination angle (from positive Y to gravity, on the XY axis) to be greater than 90. Perhaps around 135 (90 + 45 down).
We expect the azimuth angle (around the Y axis, from positive Z to gravity, in the direction of the right hand rule) to be a bit more than 90.
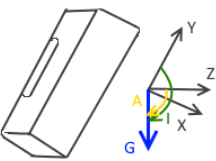
This setup resulted in this payload: 9c7db451
{
"type": "status",
"inTrip": false,
"batV": 3.092,
"temp": 22.5,
"manDown": false,
"inclinationDeg": 135,
"azimuthDeg": 121.5,
"xyz": {
"downUnit": [
0.6029,
-0.7071,
-0.3695
],
"azimuthDeg": [ left out ],
"inclinationDeg": [ left out ],
}
}
The inclination angle is the estimated 135 (90 + 45 down).
The azimuth angle is harder to visualize from the image, but is greater than 90, but less than (90 + 45).
